Макроэкономика: Совокупный спрос потребителей.
Неоклассическая функция спроса. (Связь потребления с предложением труда.)

В течение длинного временного интервала потребитель имеет возможности повлиять на свой доход, например, чтобы увеличить свой доход, он может начать трудится больше. (При этом в длинном периоде весь предложенный трудовой ресурс будет использован фирмами, так как из-за гибкости заработной платы в длинном периоде возможна лишь небольшая безработица, не связанная с избытком предложения. Подробнее.) Из этого предположения и исходит неоклассическая теория потребительского спроса. Точнее, неоклассическая теория потребления и сбережения предполагает, что человек определяет одновременно объем своего предложения труда и объем сбережения, таким образом, чтобы максимизировать полезность потребления в течение всей жизни.

Будем рассматривать всего два периода времени, в течение первого из которых индивид работает и сберегает, а во втором – нет, и расходует свои сбережения. В этой модели будем считать, что все свое время t в первом периоде человек делит на две части: рабочее время и отдых, x. В результате доход потребителя в первом периоде определяется заработной платой w и рабочим временем :

Исключим из рассмотрения налоги и инфляцию, а затем предположим, что полезность потребителя определяется функцией :

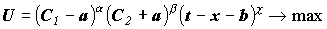
Если считать заработную плату w и процентную ставку i экзогенными параметрами модели (т.е. не зависящими от предложения труда со стороны потребителя), тогда для максимизации двухпериодной полезности потребитель может изменять свое рабочее время и потребление в первом периоде. В это же время потребление во втором периоде определяется бюджетным ограничением:

Где во вторых скобках из правой части уравнения находится объем сбережений потребителя в первом периоде. То есть бюджетное уравнение говорит нам, что расходы потребителя во втором периоде равны сбережениям потребителя в первом периоде плюс доход от инвестирования этих сбережения.

Таким образом, потребитель решает задачу максимизации функции полезности при одном ограничении. Получить решение этой задачи можно, использовав метод неопределенных множителей Лагранжа. В результате, получится такая зависимость потребления и отдыха в первом периоде от параметров потребительских предпочтений, входящих в функцию полезности, (α, β, γ, a, b), бюджета времени t и экзогенно заданных цен факторов производства i и w :

Обратите внимание, что увеличение процентной ставки приводит не только к росту склонности потребителя к сбережению, который эквивалентен снижению потребления в начальном периоде, но и к уменьшению продолжительности отдыха в этом периоде, что можно объяснить тем, что увеличивая отдачу от сбережений, растущая процентная ставка повышает (в некоторой степени) отдачу от доходов в первом периоде (т.е. их полезность), а значит, повышает ценность труда и рабочего времени.

Если учитывается сразу несколько периодов, тогда (по аналогии с вышеописанной моделью) можно сделать вывод, что склонность потребителя к сбережению определяется тем, является ли увеличение его доходов регулярным или нет. Если увеличение будет регулярным, тогда потребление возрастет примерно пропорционально росту дохода, если же доход возрастает только в одном периоде, тогда потребление останется практически на том же самом уровне, но сбережение в том периоде, когда наблюдается рост доходов, возрастет примерно на величину прироста доходов.

Итак, неоклассическая теория потребления считает, что величина потребления является функцией заработной платы и процентной ставки, которые для него являются экзогенными параметрами :

Нужна дополнительная информация по теме? Попробуйте следующее:

Модели, обосновывающие вид функции долгосрочного потребительского спроса. Продолжение.

Потребительский спрос и ожидания. Потребительский спрос и неопределенность.

Расширенная версия параграфа

Вернуться в раздел: Совокупный спрос потребителей.