Макроэкономика: Модели экономического цикла.
Экономический цикл, как следствие борьбы за распределение национального дохода. Модель P. Гудвина.

В модели Гудвина экономический цикл, так же как и в модели Крафта - Вайзе, порождается постоянным перераспределением национального дохода между работниками и предпринимателями.

Модель Гудвина – модель растущей экономики с гибкими ценами, в которой происходит постоянный рост национального дохода за счет роста населения с темпом n и роста производительности труда с темпом a. При таком типе экономического роста (если достигнуто долгосрочное экономическое равновесие) наблюдается равенство темпов прироста национального дохода и капитала, поскольку поддерживается постоянная производительность капитала. В этой экономике постоянно существует равновесие на всех рынках, что выражается в постоянном равенстве инвестиций и сбережений при фиксированной равновесной процентной ставке, которая не меняется во времени.

Введем обозначения: d – доля труда в национальном доходе, т.е. w L : y ;
q – производительность труда, т.е. y : L;
v – уровень занятости, т.е. единица минус u;
h – капиталоемкость национального дохода, т.е. y : K;
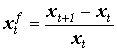– темп прироста показателя x в периоде t.

Основным объектом анализа в модели Гудвина является доля труда в национальном доходе. Темп прироста доли труда в национально продукте можно записать в виде :

Теперь, поскольку темп прироста реальной заработной платы напрямую зависит от уровня занятости, то мы можем записать :

Из определения уровня занятости следует, что темп прироста показателя занятости задается уравнением :

С учетом того, что темп прироста национального дохода в модели совпадает с темпом роста капитала, а также учитывая прямую пропорциональность между занятостью и национальным доходом, получаем :

Из записанных выше уравнений вытекает еще одно дифференциальное уравнение, задающее связь между занятостью и долей труда в национальном доходе (второе уравнение в системе). В результате поведение экономики в координатах “занятость – доля труда в НД” полностью определяется системой из двух дифференциальных уравнений :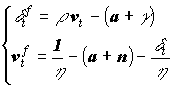

Эта система уравнений показывает, что рост занятости приводит к ускорению роста доли зарплаты в национальном доходе, но рост доли зарплаты в национальном доходе замедляет рост занятости, поскольку падают инвестиции, а значит и темп найма работников.

Данная система дифференциальных уравнений относится к классу моделей антагонистических взаимоотношений “хищник – жертва”, и описывает постоянное движение по эллиптической траектории вокруг стационарной точки :

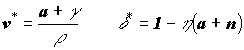
Нужна дополнительная информация по теме? Попробуйте следующее:

Экономический цикл, как следствие борьбы за распределение национального дохода. Модель Крафта – Вайзе.

Итог. Причины возникновения экономического цикла. Причины, мешающие прекращению циклических колебаний экономики.

Расширенная версия параграфа

Вернуться в раздел: Модели экономического цикла.